대표적인 정렬 알고리즘 6가지를 요약 정리해보자.
이 글은 요약정리용이므로, 자세한 글은 참고 자료를 통해 이미지와 함께 작성된 글을 확인할 수 있다.
Selection Sort (선택 정렬)
- n번의 비교과정이 필요하다.
- 최악의 경우 O(n)의 시간복잡도를 갖는다.
정렬 방법
1. 각 루프마다 최대 원소를 찾는다.
2. 최대 원소와 맨 오른쪽 원소를 교환한다.
3. 맨 오른쪽 원소를 제외한다.
4. 하나의 원소만 남을 때까지 1~3과정을 반복한다.
Bubble Sort (버블 정렬)
정렬 방법
1. 가장 왼쪽부터 서로 인접한 두 원소를 검사하여 정렬한다.
2. 인접한 2개의 원소를 비교해 크기가 큰 값을 오른쪽으로 옮긴다.
3. 한 번의 루프가 끝나면, 가장 큰 값을 제외하고 1~2과정을 수행한다.

Insertion Sort (삽입 정렬)
정렬 방법
1. 맨 처음 인덱스의 원소를 정렬된 상태라고 본다.
2. 두번째 인덱스에 있는 데이터를 이 정렬된 배열에 삽입하면서 두 데이터가 다시 정렬된 방법으로 만든다.
3. 1~2과정을 반복한다.
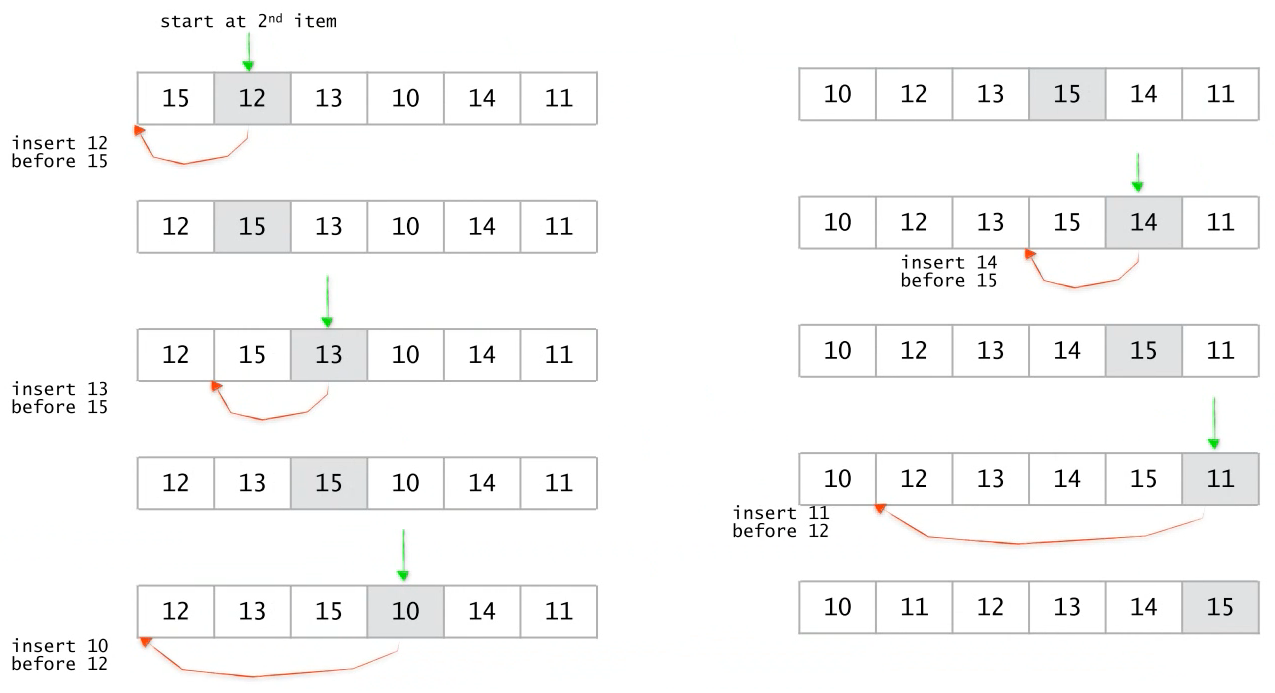
삽입, 버블, 선택정렬 참고 자료
- https://ict-nroo.tistory.com/52?category=698685
- https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
- https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
- https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
Merge Sort (합병 정렬)
- Merge Sort는 분할 정복 알고리즘을 사용한다.
- 기본적으로 순환 호출을 사용해 문제를 하결한다.
- 최악의 경우 O(nlogn)의 시간복잡도를 갖는다.
정렬 방법
0. 리스트의 길이가 0또는 1이면 정렬된 것으로 본다. -> return;
1. 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
2. 나뉘어진 부분 배열을 정렬한다.
3. 1~2과정을 부분 배열의 크기가 충분히 작을 때까지 (0,1) 반복한다.
4. 정렬된 부분 배열들을 하나의 배열에 합병한다.
5. 합병 시 2개의 리스트 값들을 처음부터 하나씩 비교하여 두 리스트의 값 중에서 더 작은 값을 새로운 리스트로 옮긴다.
6. 둘 중 하나가 끝날 때까지 이 과정을 되풀이한다.
7. 하나가 먼저 끝나면 나머지 리스트를 통째로 복사한다.
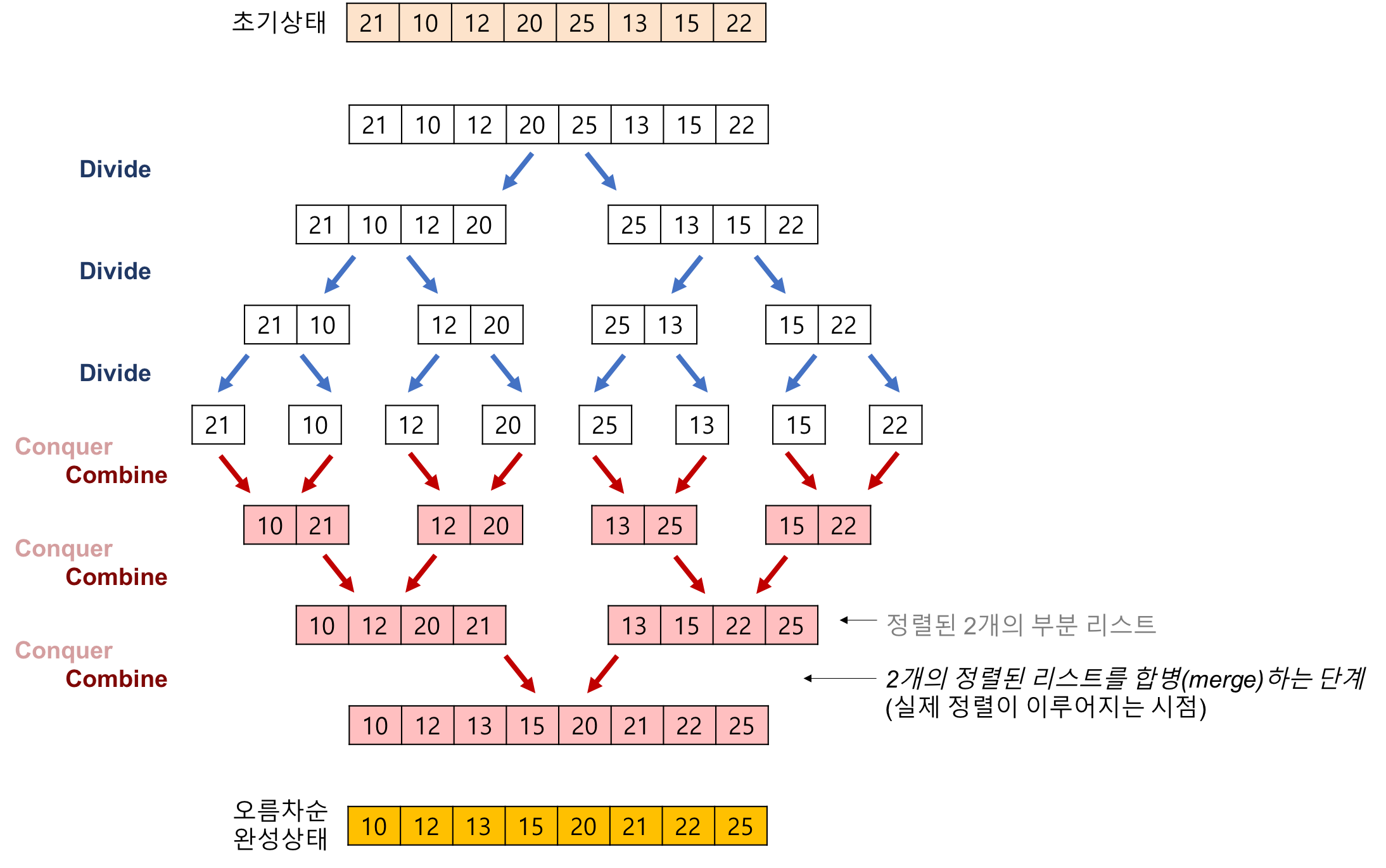
참고 자료
- https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
- https://ict-nroo.tistory.com/53?category=698685
Quick Sort (빠른 정렬)
- Quick Sort는 비교 정렬 방법 중의 분할 정복 알고리즘을 사용한다.
- 평균적으로 매우 빠른 속도를 갖는다.
- 최악의 경우 O(nlogn)의 시간복잡도를 갖는다.
- 분할
- 배열을 기준값을 기준으로 하여 조건을 만족하도록 두 부분으로 나눈다.
- 즉, 기준 값(pivot)을 기준으로 작은 값, 큰 값으로 구분한다.
- 정복
- 값들을 순환 호출해 정렬한다.
정렬 방법
1. 리스트 안의 한 요소를 선택해 기준값(pivot)으로 삼는다.
2. 피벗을 기준으로 피벗보다 작은 값은 왼쪽으로, 피벗보다 큰 값은 오른쪽으로 옮긴다.
3. 피벗을 제외한 왼쪽리스트, 오른쪽 리스트를 다시 정렬한다.
- 이때, 왼쪽 리스트와 오른쪽 리스트 각각에 대해 1~3 과정을 수행한다.
4. 이 과정을 리스트가 더 이상 분할 불가능할 때까지 (리스트의 크기가 0이거나 1이 될 때까지) 반복한다.
참고 자료
- https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
- https://ict-nroo.tistory.com/54?category=698685
Heap Sort (힙정렬)
- 최대힙이나 최소힙을 구성해 정렬하는 방법
- 내림 차순을 위해서는 최대힙 / 오름 차순을 위해서는 최소힙을 구성하면 된다.
- 전체 자료 정렬보다는 가장 큰 값 몇개만 필요할 때 힙을 구성한 뒤 정렬하면 유용한 방법으로 사용할 수 있다.
- 최악의 경우에 시간복잡도 O(nlogn)을 갖는다.
- 시간 복잡도가 O(nlogn)을 가지면서, merge sort처럼 추가 배열을 필요로 하지 않기에 좋은 정렬 알고리즘이다.
정렬 방법
1. 정렬해야할 n개의 요소들로 힙을 만든다.
2. 한번에 하나씩 요소를 힙에서 꺼낸 뒤, 배열의 뒤(앞)부터 저장되게 한다.
3. 삭제되는 요소들은 값이 감소되는 순서로 정렬되게 한다.
참고 자료
- https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
- https://ict-nroo.tistory.com/55?category=698685
정렬 알고리즘 시간 복잡도 비교

![[알고리즘] 정렬 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FlMcch%2Fbtrdr3cUm8V%2FAAAAAAAAAAAAAAAAAAAAAFeZBCJXttFMZetUBWwDYzX3e4CZgoHzM9wSid9pYDe0%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1753973999%26allow_ip%3D%26allow_referer%3D%26signature%3DNIOM%252BxDkqtuT0ACDpusn1Qq4jj0%253D)